NATO Advanced Research Workshop
on
Systematic Organization of Information in Fuzzy Systems
24-26 October 2001, Vila Real, Portugal (PST.978173)
This list includes the titles of the lectures to be presented in the ARW and the links to electronic copies of the abstracts and papers sent by the authors. The Program of the ARW is also included for convenience.
Main program of the ARW (small last hour changes may occur)
L. Zadeh: Toward a Perception-Based Theory of Probabilistic Reasoning
(This presentation will be scheduled according to the disponibility of Prof. Zadeh. Therefore, small changes in the program may occur.)
October 24
a.m. 9:30 - 10:45 Klir, G.: Uncertainty-Based Information
11:00 - 11:45 Yager R.: Organization of Fuzzy Information
12:00 - 13:00 Short presentation by participants + Discussion (3x20min per person) . Moderator: J. Baldwin
p.m. 14:30 - 15:45 Baldwin J.: Mass Assignment Theory for Fuzzy Bayesian Nets (.pdf file
)
16:00 - 18:00 Short presentations by participants + Discussion (6x20min per person) . Moderator: T. Fukuda
October 25
a.m. 9:30 - 10:45 Rudolf Kruse, Information Mining with Relational and Possibilistic Graphical Models (PowerPoint file)
11:00 - 11:45 Teodorescu H.N.: Neuro-fuzzy Information Processing and Self Organization in Dynamic Systems
12:00 - 12:40 Short presentations by participants + Discussion (2x20min per person). Moderator: G. Klir
p.m. 14:30 - 15:45 Fukuda T.: Fuzzy Control
16:00 - 18:00 Short presentation by participants + Discussion (6x20min per person) . Moderator: A. Kandel
October 26
a.m. 9:30 - 10:45 A. Kandel: Automated Quality Assurances of Continuous Data
11:00 - 12:40 Short presentation by participants + Discussion (5x20min per person) . Moderator: C. Couto
p.m. 14:15 - 16:15 Zadeh L. (chairman): Panel discussion and final conclusions
List of invited participants
Prof. Krassimir T. Atanassov, Bulgarian Academy of Sciences, Bulgary ( Intuitionistic fuzzy generalized nets and intuitionistic fuzzy systems)
Prof. Dan Cristea, University "Al.I. Cuza" of Iasi, Romania (will discuss issues related to natural languages)
Prof. Paulo Jorge Ferreira, Universidade de Aveiro, Portugal
Dr. Constantin Gaindric, Institute of Math. and Computer Science, Moldova ( Fuzzy evaluation processing in decision support systems)
Dr. Xiao-Zhi Gao, Helsinki University of Technology, Finland ( DFSLIF: Dynamical fuzzy systems with linguistic information feedback)
Miroslaw Kwieselewicz, Technical University of Gdansk, Poland (A methodology for incorporating human factors in fuzzy-probabilistic modelling and risk analysis of industrial systems)
Prof. Drago Matko, Faculty of Elect. Engineering, Ljubljana, Slovenia ( Systematic approach to nonlinear modeling using fuzzy techniques)
Prof. Carlo Morabito, University Reggio Calabria, Italy (Environmental Data Interpretation: The Next Challenge For Intelligent Systems.)
Prof. Nikolai G. Nikolov, Bulgary (presentation together with Prof. Atanassov)
Prof. Walenty Ostasiewicz, Poznan University, Poland (announced topic:
Uncertainty and Vagueness in Information -
.pdf file)
Prof. Rita Almeida Ribeiro, Universidade Nova, Portugal ( Fuzzy hierarchical aggregation for number recognition)
Dr. Luis Rocha, Los Alamos National Laboratory, USA (Presentation will be available as movies)
Prof. Paulo Salgado, University Tras-os-Montes Alto Douro, V. Real, Portugal (Relevance of the fuzzy logic sets and systems)
Dr. Adrian Stoica, JPL, NASA ( Evolutionary synthesis of fuzzy circuits)
Prof. Ioan Tofan, University "Al.I. Cuza" of Iasi, Romania (tentative topic: Algebraic aspects of fuzzy information organization and aggregation)
Prof. Friedrich Steimann, University of Hannover, Germany (Fuzzy information in medicine - presentation to be available at the ARW)
Prof. J.L.. Verdegay, University of Granada, Spain (Fuzzy sets-based heuristics)
INTUITIONISTIC FUZZY GENERALIZED NETS AND INTUITIONISTIC FUZZY SYSTEMS
K. Atanassov
(Abstract)
Generalized Nets (GNs) are extensions of Petri
nets and Petri net modifications and extensions. The concept of GN was defined
in 1982 (see [1]). Their transitions have two temporal components (moment of
transition firing and its duration), two indexed matrices (the (i,j)-th element
of the first one is a predicate that determines whether a token from i-th input
place can be transfered to j-th output place; the (i,j)-th element of the second
one determines the capacity of the arc between the same two places). The GN
have three global time-components: moment of GN-activation,elementary time-step
and duration of the GN-functioning. The GN-tokens enter the GN with initial
characteristics and at the time of their transfer in the net they obtain next
(current and final) characteristics. A lot of operations, relations and operators
(global, local, dynamical, and others) are defined over the GNs.
The Intuitionistic Fuzzy Sets (IFSs), defined in 1983, are extensions of the
fuzzy sets (see [2]). They have two degrees - degree of membership (M) and degree
of non-membership (N) such that their sum can be smaller that 1, i.e., a third
degree - of uncertainty (U = 1 - M - N) can be defined, too. A lot of operations,
relations and operators (from modal, topological and others types) are defined
over the IFSs. The GNs already have a lot (more than 20) of extensions. The
first of them, published in 1985 (see [3]), was called Intuitionistic Fuzzy
GN (IFGN). The transition condition predicates of these nets are estimated in
intuitionistic fuzzy sense. Latter, this extension was called IFGN of a first
type, because IFGN of a second type was defined. In it, tokens are replaced
by "quantities" that flow within the net. Now places, instead of tokens, obtain
characteristics. Both GN extensions (as it is done for all other GN-extensions)
are proved to be conservative ones of the ordinary GNs.
A third type of IFGNs will be defined and their properties will be discussed.
Now, not only the transition condition predicates and the form of the tokens
can be fuzzy, but also, the tokens characteristics, too. Intuitionistic Fuzzy
Abstract System (IFAS) is an abstract system in Mesarovic and Takahara's sense,
the behaviour of whose components and of it in general is estimated in IFS sense
(see [2]). Some modifications of IFAS will be discussed with respect to the
representation of elements of Artificial Intelligence (expert systems, machine
learning processes and others) by IFASs. Some applications of the IFGNs from
the three types and of the IFASs will be discussed.
References:
[1] Atanassov, K. Generalized Nets. World Scientific, Singapore, New Jersey, London, 1991.
[2] Atanassov, K. Intuitionistic Fuzzy Sets. Springer, Heidelberg, 1999.
[3] Atanassov K., Generalized nets and their fuzzings, AMSE Review, Vol. 2 (1985), No. 3, 39-49.
FUZZY EVALUATION PROCESSING IN DECISION SUPPORT SYSTEMS
Constantin Gaindric
Abstract
We propose an algorithm of forming orders portfolio when the funds are limited and multicriterion evaluations of projects by experts are fuzzy. The algorithm is used in DSS for planning of financing of scientific researches.
Keywords: Fuzzy evaluation, Decision support systems.
Full text
(In case
you are unable to see the document when clicking on the link, please use the
right-hand mouse button to save the document on your disk, then open the .pdf
file from your disk).
A DYNAMICAL FUZZY SYSTEM WITH LINGUISTIC INFORMATION FEEDBACK
X. Z. Gao, S. J. Ovaska
Abstract
In this paper, we propose a new dynamical fuzzy system with linguistic information feedback. Instead of crisp system output, the delayed fuzzy membership function in the consequence part is fed back locally with adjustable parameters in order to overcome the static mapping drawback of conventional fuzzy systems, as shown in Fig. 1.
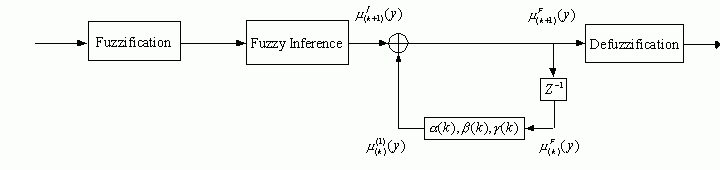
Fig. 1. Structure of dynamical fuzzy system with linguistic information feedback.
We give a detailed description of the corresponding structure
and algorithm. Our dynamical fuzzy system with linguistic information feedback
has several remarkable features. First, the rich fuzzy inference output rather
than crisp signals is fed back without any information transformation and loss.
Second, the local feedback loops act as internal memory units here to store
temporal input information. This is pivotal in identifying dynamical plants.
In other words, linguistic information feedback can effectively and accurately
capture the dynamics of the nonlinear systems to be modeled. Third, training
of the three feedback coefficients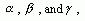 
leads
to an equivalent update of those membership functions for output variables.
Actually, it can be regarded as a kind of implicit parameter adjustment in this
fuzzy system, and thus adds the advantage of self-adaptation to our model. Simulation
experiments have been carried out to demonstrate effectiveness of the proposed
dynamical fuzzy system in time sequence prediction.
PowerPoint presentation (In case you are unable to see the document when clicking on the link, please use the right-hand mouse button to save the document on your disk, then open the .pdf file from your disk).
AUTOMATED QUALITY ASSURANCES OF CONTINUOUS DATA
Abraham Kandel
Abstract
Most real-world databases contain some amount of inaccurate data.reliability of critical attributes can be evaluated from the values of other attributes in the same table. This paper presents a new fuzzy-based measure of data reliability in conyinuous attributes. We partition the relational schema of a database into a subset of input (predicting) and a subset of target (dependent) attributes. A data mining model, called information-theoretic connectionist network, is constructed for predicting the values of a continuous target attribute. The network calculates the degree of reliability of the actual target values in each record by using their distance from predicted values. The approach is demonstrated on the voting data from the 2000 Presidential Election in the US.
Full text (In
case you are unable to see the document when clicking on the link, please use
the right-hand mouse button to save the document on your disk, then open the
.pdf file from your disk).
A METHODOLOGY FOR INCORPORATING HUMAN FACTORS IN FUZZY-PROBABILISTIC MODELLING AND RISK ANALYSIS OF INDUSTRIAL SYSTEMS
Miroslaw Kwieselewicz, Kazimierz T. Kosmowski
Abstract
The paper addresses some methodological aspects of fuzzy-probabilistic modelling
of complex hazardous industrial systems. Due to several sources of uncertainty
involved in risk evaluations and necessity to incorporate human and organisational
factors, a fuzzy-probabilistic modelling framework is proposed for handling
uncertainty. A methodology has been developed for systematic incorporating these
factors into the risk model. Proposed methodology is a synthesis of techniques
for performing human reliability analysis (HRA) in the context of probabilistic
safety analysis (PSA) based on available quantitative and qualitative information.
Human and organisational factors are nested in a hierarchical structure called
influence diagram in a similar way as in analytic hierarchy process (AHP) methodology.
Several levels of hierarchy are distinguished: direct, organisational, regulatory
and policy. Systematic procedure for weighting and scaling of these factors
in this hierarchical structure has been proposed.
The approach enables a systematic functional/structural decomposition of the
plant. For this purpose three basic methods are used: event trees (ETs) and
fault trees (FTs) and influence diagrams (IDs). Events of human errors are represented
in FTs and / or, but indirect human factors are incorporated in hierarchical
structures of IDs. Human error events can be latent, due to the design deficiencies
or organisational inadequacies, and active committed by human operators in the
course of accident. A method proposed for evaluation of human component reliability
is a generalisation of SLIM technique for a hierarchy of factors.
The paper emphasises that PSA and related HRA are performed in practice for
representative events: initiating events, equipment/ human failures, and accident
sequences (scenarios) that represent categories of relevant events. Transitions
of the plant states in accident situations can not be assumed always as random.
Taking into account limitations of the Bayesian framework it is proposed to
apply for the uncertainty modelling a fuzzy-probability method and when justified
the fuzzy interval framework related to the possibility theory. The paper also
outlines a method of cost-benefit analysis of risk-control options (RCOs) in
comparison with a basis option (B) for representative values of the fuzzy intervals.
RCOs considered are raked based on defined effectiveness measure. At the end
of the paper some research challenges in the domain are shortly discussed.
The methodology proposed has been developed in a research project within the
Strategic Government Programme (SPR-1), in the period of 1998-2000, aimed at
developing methods and computer tools for supporting risk analyses and safety
management of hazardous industrial systems.
UNCERTAINTY-BASED INFORMATION
George J. Klir
Abstract
It is argued that scientific knowledge is organized, by and large, in terms
of systems of various kinds. In general, systems are viewed as relations among
states of some variables. Employing the constructivist viewpoint, it is recognized
that systems are constructed from our experiential domain for various purposes,
such as prediction, retrodiction, prescription, diagnosis, planning, control,
etc. In each system, its relation is utilized, in a given purposeful way, for
determining unknown states of some variables on the basis of known states of
other variables. Systems in which the unknown states are determined uniquely
are called deterministic; all other systems are called nondeterministic. By
definition, nondeterministic systems involve uncertainty of some type. This
uncertainty pertains to the purpose for which the system was constructed. It
is thus natural to distinguish predictive uncertainty, retrodictive uncertainty,
diagnostic uncertainty, etc. In each nondeterministic system, the relevant uncertainty
must be properly incorporated into its description in some formalized language.
It is shown how the emergence of fuzzy set theory and the theory of monotone
measures considerably expanded the framework for formalizing uncertainty. A
classification of uncertainty theories that emerge from this expanded framework
is examined. It is argued that each of these theories needs to be developed
at four distinct levels: (i) representation of the conceived type of uncertainty;
(ii) calculus by which this type of uncertainty can be properly manipulated;
(iii) measuring, in a justifiable way, the amount of relevant uncertainty (predictive,
prescriptive, etc.) in any situation formalizable in the theory; and (iv) various
uncertainty principles and other methodological aspects.
In general, uncertainty-based information is defined in terms of uncertainty
reduction within a given experimental frame in terms of which a particular system
was constructed. Uncertainty reduction can only be produced by an appropriate
action. The amount of uncertainty-based information produced by an action is
measured by the amount of uncertainty that is reduced by the action. That is,
uncertainty-based information is expressed in terms of the difference between
a priori and a posteriori uncertainties.
Only some of the various uncertainty theories emerging from the expanded framework
have been thoroughly developed thus far. They include possibility theory, Dempster-Shafer
theory of evidence, uncertainty formalized in terms of Sugeno l-measures, and
several types of theories of imprecise probabilities. Results regarding these
theories at the four mentioned levels (representation, calculus, measurement,
methodology) are surveyed.
SYSTEMATIC APPROACH TO NONLINEAR MODELING USING FUZZY TECHNIQUES
D. Matko
Abstract
The paper deals with the systematic approach of using Fuzzy Models as universal approximators. Four types of models suitable for identifi cation are presented: The Nonlinear Output Error, The Nonlinear Input Error, The Nonlinear Generalized Output Error and The Nonlinear Generalized Input Error Model. The convergence properties of all four models in the presence of disturbing noise are reviewed and it is shown that the condition for an unbised identification is that the disturbing noise is white and that it enters the nonlinear model in specific point depending on the type of the model. The aplication of the proposed modelling approach is illustrated with a fuzzy model based control of a laboratory scale heat exchanger.
Full text (In
case you are unable to see the document when clicking on the link, please use
the right-hand mouse button to save the document on your disk, then open the
.pdf file from your disk).
ENVIRONMENTAL DATA INTERPRETATION: THE NEXT CHALLENGE FOR INTELLIGENT SYSTEMS.
Franco Carlo Morabito
Abstract
Environmental data processing is based on modelling and prediction of time series whose dynamic evolution is the result of the concurrence of many variables. The goal of this presentation is to show some recent advances in data driven approaches (like Artificial Neural Networks, ANN, and Fuzzy Inference Systems, FIS) to environmental problems solution. These intelligent systems can be useful in various contexts: to perform knowledge discovery in large environmental databases ("environmental data mining"), to make prediction, to explain and interpret data and non linear correlation among predicting variables. The output of the intelligent processing systems can also facilitate decision making. Environmental data show some characteristics features and peculiarities (noise, non linearity, non-stationarity, missing data, …) that largely justifies the use of data oriented models. Here are some specific open ended issues in environmental monitoring (water, air and soil pollution) which require a modern approach for their assessment: identification and diagnosis of a given situation based on the processing of time and spatially varying data; forecasting regular event (short time); forecasting of rare end extreme events (mid and long time); evaluation of a solution; inverse modelling. The paper will illustrate real practical applications in which intelligent systems have been deliberately introduced in the processing chains to solve problems that appears to be "unsolvable" by making use of more traditional statistical and model-based approaches. The presentation will hopefully stimulate a wide interest on environmental data analysis and monitoring within the framework of supervised and unsupervised learning.
RELEVANCE OF THE FUZZY LOGIC SETS AND SYSTEMS
Paulo Salgado
Abstract
The readability of the fuzzy models is related to its organizational structure
and the correspondent rules base. A new paradigm for the description of a system
model using fuzzy IF…THEN rules is proposed in this paper. In order to define
methodologies for organizing the information describing a system, it is important
to specify metrics that define the relative importance of a set of rules in
the description of a given region of the input/output space. The concept of
relevance proposed herein enables this measurement. This concept is defined
by a set of intuitive axioms, leading to a set of properties that any function
of relevance must obey. Considering this, a new methodology for organizing the
information was developed entitled Separation of Linguistic Information Methodology
(SLIM). Based on these results, different algorithms were proposed for different
structures, which one with various layers: the Parallel Collaborative Structure
(PCS) - SLIM-PCS algorithm; the Hierarchical Prioritized Structure (HPS), proposed
by Yager, SLIM-HPS algorithm; and the General Structure (GS).
Finally, a new Fuzzy Clustering of Fuzzy Rules Algorithm (FCFRA) is proposed.
Typically, the FCM (Fuzzy C-means) algorithms organize clusters of points with
same similarity. Similarly, the FCFRA organize the rules of a fuzzy system in
various sub-fuzzy systems, interconnected in a structure. Its application in
the organization of information of fuzzy system in HPS and CPS structures are
demonstrated as well. In addition, the SLIM methodology and the different algorithm
have been successfully applied to modeling different systems, namely real systems.
EVOLUTIONARY SYNTHESIS OF FUZZY CIRCUITS
Adrian Stoica
Abstract
Recent research in evolutionary synthesis of electronic circuits and evolvable
hardware [1], [2] has generated a set of ideas and demonstrated a set of concepts
that have direct application to the computational circuits used for information
processing in fuzzy systems.
This paper overviews five such concepts developed by the author:
1) evolutionary techniques for automatic synthesis of electronic circuits implementing fuzzy operators and functions;
2) re-configurable devices for fuzzy configurable computing and on-chip evolution of fuzzy systems;
3) mixtrinsic evolution for automatic modeling/identification of correlated fuzzy models of different granularity/resolution/flavor;
4) accelerating circuit evolution (and modeling in general) through gradual morphing through fuzzy topologies;
5) polymorphic electronics as circuits with superimposed multiple functionality, in particular fuzzy functionality.
Full text (In
case you are unable to see the document when clicking on the link, please use
the right-hand mouse button to save the document on your disk, then open the
.pdf file from your disk).
FUZZY HIERACHICAL AGGREGATION FOR NUMBER RECOGNITION
R. A. Ribeiro
Abstract
In this paper we use a fuzzy hierarchical aggregation method for voice recognition of the Portuguese numbers from 0 to 9. To obtain the parameters we have a recognition process that uses a linear predictive coding model to define the signal window and two auto regression analysis methods to obtain the parameters. Further, two other parameters are also collected, the time t of the signal and the number of syllables of the speech. After obtaining the parameters a fuzzy aggregation method is used. First, the parameters are transformed into fuzzy sets using triangular membership functions. Second, a hierarchy of the attributes (parameters) is built using the Analytical Hierarchy Process of Saaty [1]. Third, we use the Ordered Weighted Averaging (OWA) operators [2] to perform the hierarchical aggregation of parameters and respective importances. An example is shown to illustrate how this approach seems suitable for voice recognition of numbers.
NEURO-FUZZY INFORMATION PROCESSING AND SELF ORGANIZATION IN DYNAMIC SYSTEMS
Horia-Nicolai Teodorescu
Abstract
In this lecture, I address the issue of self-organization of information in fuzzy and neuro-fuzzy dynamical systems. Applications of the information self-organization in fuzzy systems range from modeling and information retrieval to knowledge discovery. It is well known that in large dynamical systems, self-organization processes frequently occur. Such systems are, among others, the neural networks (either natural or artificial). The first paradigm introduced in this lecture is the use of dynamical self-organization to retrieve information or to extract knowledge. The second paradigm is to use dynamical fuzzy systems to organize and retrieve information that inerently carries imprecision or uncertainty, or to evidence knowledge about imprecise processes. In the first part of the lecture, basic concepts on dynamical fuzzy systems (DFS), and "fuzzy chaos" are presented. The second section is devoted to the self-organization of the fuzzy processes in dynamical fuzzy systems. The third section is devoted to the information retrieval and knowledge discovery processes as carried out in DFSs, and to potential applications. The use of evolutionary algorithms in adapting the DFSs addressed in view of achieving information self-organization is also briefly addressed.
Keywords: dynamic fuzzy system, neuro-fuzzy system, information organization, self-organization system, knowledge discovery, evolutionary algorithms.
Contents:
1. Background
2. Self-organization in dynamical systems
3. Dynamic fuzzy systems: basic concepts
4. Dynamic neuro-fuzzy systems
5. Information organization in DFS
6. Information retrieval based on DFS
7. Knowledge discovering using DFS
8. Applications and further issues
9. Conclusions
ALGEBRAIC ASPECTS OF INFORMATION ORGANISATION
Ioan Tofan
Abstract
We deal with the problem of information organization from the
viewpoint of generalized structures (fuzzy structures and hyperstructures).
The fuzzy quantitative information can be modelled by fuzzy numbers, while the
fuzzy qualitative information can be modelled by hyperstructures, in the sense
that, for example, two (vague) informations yield a set of possible consequences.
The similarity relations (fuzzy generalizations of equivalence relations) are
in direct connection with shape (pattern) recognition.
The significance of information appears most clearly in structures; this induces
the necessity of studying the fuzzy algebraic structures (fuzzy groups, rings,
ideals, subfields and so on) as a means towards the better understanding and
processing of information. The theory of algebraic hyperstructures has surprising
connections with the fuzzy structures, which can be interpreted as connections
between quantitative and qualitative information.
This report presents some recent results and methods in the rapidly growing
fields of fuzzy algebraic structures and hyperstructures and some connections
between them. Some results on fuzzy groups, fuzzy rings and fuzzy subfields
are given. Likewise, the consideration of diverse sets of fuzzy numbers and,
more notably, of the structures that these sets can be endowed with is of utmost
importance. In this direction, the operations with fuzzy numbers play a major
role and a number of questions regarding these operations are still open. A
sample of the different notions of fuzzy number and of the operations with fuzzy
numbers and their properties is given in this report. Diverse types of similarity
classes an partitions are studied. Several notions of f-hypergroup, which combine
fuzzy structures and hyperstructures, are presented and studied. Some results
that put forward a two-way connection between L-fuzzy structures and hyperstructures
are given.
Full text (In
case you are unable to see the document when clicking on the link, please use
the right-hand mouse button to save the document on your disk, then open the
.pdf file from your disk).
FUZZY SETS-BASED HEURISTICS
Jose L. Verdegay
Abstract
The main aim of this paper is to show how fuzzy sets and systems can be used to produce optimization algorithms able of being applied in a variety of practical situations. In this way, and on the one hand, fuzzy sets based heuristics for Linear Programming problems are considered. To show the practical realisations of the proposed approach, the Travelling Salesman Problem is assumed, and a new heuristic proving the efficiency of using fuzzy rules as termination criteria is shown. On the other hand, the basic ideas of a Fuzzy Adaptive Neighborhood Search (FANS) heuristic algorithm are also presented. Its main motivation is to provide a general purpose optimization tool, which is easy to tailor to specific problems by means of appropriate definition of its components. The Knapsack Problem with multiple constraints will serve to show the high solution potential of this another fuzzy sets based heuristic algorithm.
Keywords: Heuristics, Knapsack Problem, Fuzzy Rules, Fuzzy Sets and Systems, Travelling Salesman Problem, Linear Programming, Genetic Algorithms, Simulated Annealing, Decision Support Systems.
Full Text (In
case you are unable to see the document when clicking on the link, please use
the right-hand mouse button to save the document on your disk, then open the
.pdf file from your disk).
ORGANIZATION OF FUZZY INFORMATION
Ronald Yager
Abstract
Here we look at a number of methods of organizing information and knowledge.
Particular attention will paid to hierarchical structures and the operations
needed to process this type of information. One structure we shall discuss is
the Hierarchical Prioritized Structure (HPS). This structure provides a framework
for a hierarchical representation of a fuzzy rule base by assigning rules to
different levels in the hierarchy in a way that allows for a natural learning
mechanism . An important part of this structure is the Hierarchical Updation
(HEU) aggregation operator. This new aggregation operation allows for implementation
of the rules in a prioritized fashion, lower priority rules are only implemented
if no relevant higher priority rule is available.
We shall also discuss another hierarchical structure one that can be used in
the task of retrieving information on the internet. Using this structure we
able to define complex search requirements in terms of simple attributes that
enables an aitumated system to determine a documents satisfaction to the requirements.
TOWARD A PERCEPTION-BASED THEORY OF PROBABILISTIC REASONING
Lotfi Zadeh
(Extended Abstract)
The past two decades have witnessed a dramatic growth in the use of probability-based
methods in a wide variety of applications centering on automation of decision-making
in an environment of uncertainty and incompleteness of information.
Successes of probability theory have high visibility. But what is not widely
recognized is that successes of probability theory mask a fundamental limitation--the
inability to operate on what may be called perception-based information. Such
information is exemplified by the following. Assume that I look at a box containing
balls of various sizes and form the perceptions: (a) there are about twenty
balls; (b) most are large; and (c) a few are small. The question is: What is
the probability that a ball drawn at random is neither large nor small? Probability
theory cannot answer this question because there is no mechanism within the
theory to represent the meaning of perceptions in a form that lends itself to
computation. The same problem arises in the examples:
Usually Robert returns from work at about 6:00 p.m. What is the probability that Robert is home at 6:30 p.m.?
I do not know Michelle's age but my perceptions are: (a) it is very unlikely that Michelle is old; and (b) it is likely that Michelle is not young. What is the probability that Michelle is neither young nor old?
X is a normally distributed random variable with small mean and small variance. What is the probability that X is large?
Given the data in an insurance company database, what is the probability that my car may be stolen? In this case, the answer depends on perception-based information that is not in an insurance company database.
In these simple examples--examples drawn from everyday experiences--the general
problem is that of estimation of probabilities of imprecisely defined events,
given a mixture of measurement-based and perception-based information. The crux
of the difficulty is that perception-based information is usually described
in a natural language--a language that probability theory cannot understand
and hence is not equipped to handle.
To endow probability theory with a capability to operate on perception-based
information, it is necessary to generalize it in three ways. To this end, let
PT denote standard probability theory of the kind taught in university-level
courses. The three modes of generalization are labeled: (a) f-generalization;
(b) f.g-generalization: and (c) nl-generalization. More specifically: (a) f-generalization
involves fuzzification, that is, progression from crisp sets to fuzzy sets,
leading to a generalization of PT that is denoted as PT+. In PT+, probabilities,
functions, relations, measures, and everything else are allowed to have fuzzy
denotations, that is, be a matter of degree. In particular, probabilities described
as low, high, not very high, etc. are interpreted as labels of fuzzy subsets
of the unit interval or, equivalently, as possibility distributions of their
numerical values; (b) f.g-generalization involves fuzzy granulation of variables,
functions, relations, etc., leading to a generalization of PT that is denoted
as PT++. By fuzzy granulation of a variable, X, what is meant is a partition
of the range of X into fuzzy granules, with a granule being a clump of values
of X that are drawn together by indistinguishability, similarity, proximity,
or functionality. For example, fuzzy granulation of the variable age partitions
its vales into fuzzy granules labeled very young, young, middle-aged, old, very
old, etc. Membership functions of such granules are usually assumed to be triangular
or trapezoidal. Basically, granulation reflects the bounded ability of the human
mind to resolve detail and store information; and (c) Nl-generalization involves
an addition to PT++ of a capability to represent the meaning of propositions
expressed in a natural language, with the understanding that such propositions
serve as descriptors of perceptions. Nl-generalization of PT leads to perception-based
probability theory denoted as PTp.
An assumption that plays a key role in PTp is that the meaning of a proposition,
p, drawn from a natural language may be represented as what is called a generalized
constraint on a variable. More specifically, a generalized constraint is represented
as X isr R, where X is the constrained variable; R is the constraining relation;
and isr, pronounced ezar, is a copula in which r is an indexing variable whose
value defines the way in which R constrains X. The principal types of constraints
are: equality constraint, in which case isr is abbreviated to =; possibilistic
constraint, with r abbreviated to blank; veristic constraint, with r = v; probabilistic
constraint, in which case r = p, X is a random variable and R is its probability
distribution; random-set constraint, r = rs, in which case X is set-valued random
variable and R is its probability distribution; fuzzy-graph constraint, r =
fg, in which case X is a function or a relation and R is its fuzzy graph; and
usuality constraint, r = u, in which case X is a random variable and R is its
usual--rather than expected--value.
The principal constraints are allowed to be modified, qualified, and combined,
leading to composite generalized constraints. An example is: usually (X is small)
and (X is large) is unlikely. Another example is: if (X is very small) then
(Y is not very large) or if (X is large) then (Y is small).
The collection of composite generalized constraints forms what is referred to
as the Generalized Constraint Language (GCL). Thus, in PTp, the Generalized
Constraint Language serves to represent the meaning of perception-based information.
Translation of descriptors of perceptions into GCL is accomplished through the
use of what is called the constraint-centered semantics of natural languages
(CSNL). Translating descriptors of perceptions into GCL is the first stage of
perception-based probabilistic reasoning.
The second stage involves goal-directed propagation of generalized constraints
from premises to conclusions. The rules governing generalized constraint propagation
coincide with the rules of inference in fuzzy logic. The principal rule of inference
is the generalized extension principle. In general, use of this principle reduces
computation of desired probabilities to the solution of constrained problems
in variational calculus or mathematical programming.
It should be noted that constraint-centered semantics of natural languages serves
to translate propositions expressed in a natural language into GCL. What may
be called the constraint-centered semantics of GCL, written as CSGCL, serves
to represent the meaning of a composite constraint in GCL as a singular constraint
X isr R. The reduction of a composite constraint to a singular constraint is
accomplished through the use of rules that govern generalized constraint propagation.
Another point of importance is that the Generalized Constraint Language is maximally
expressive, since it incorporates all conceivable constraints. A proposition
in a natural language, NL, which is translatable into GCL, is said to be admissible.
The richness of GCL justifies the default assumption that any given proposition
in NL is admissible. The subset of admissible propositions in NL constitutes
what is referred to as a precisiated natural language, PNL. The concept of PNL
opens the door to a significant enlargement of the role of natural languages
in information processing, decision, and control.
Perception-based theory of probabilistic reasoning suggests new problems and
new directions in the development of probability theory. It is inevitable that
in coming years there will be a progression from PT to PTp, since PTp enhances
the ability of probability theory to deal with realistic problems in which decision-relevant
information is a mixture of measurements and perceptions.
 Return
to NATO-ARW mainpage |
Last modified: 1 November, 2001
|
